In this post, we’ll see an implementation of shortest path finding in a graph of connected nodes using Python. The shortest path will be found by traversing the graph in breadth first order.
As a related topic, see some common Python programming mistakes.
Breadth first search
Let’s consider the following graph. We will traverse it in breadth first order starting from node 0. Our goal will be to find node x.
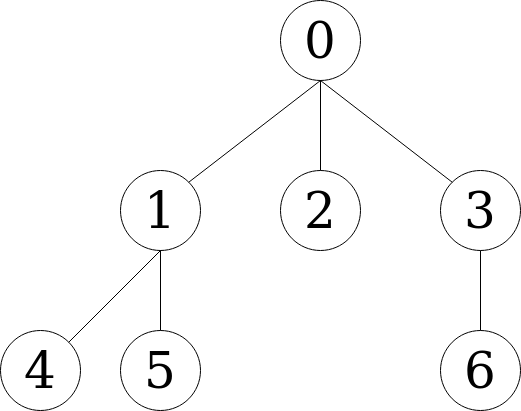
First, we will traverse the nodes that are directly connected to 0. Those are {1, 2, 3}. If node x is part of {1, 2, 3}, we stop. If not, we continue traversing the graph.
Next, we consider the set of nodes that are connected to or previous set {1, 2, 3}. Those would be {4, 5, 6}. Nodes 4 and 5 are connected to node 1 and node 6 is connected to node 3. We look for node x again and then we stop becausre there aren’t any more nodes.
If the graph was larger, we would continue traversing the graph by considering the nodes connected to {4, 5, 6} and so on.
See that this order of traversal guarantees that we find the shortest path between node 0 and node x because we start by searching the nodes that are one edge away from node1, then those that are two edges distant, and so on.
Graph representation
We will represent our graph as a dictionary, mapping each node to the set of the nodes it is connected to.
For example, let’s consider the following graph.
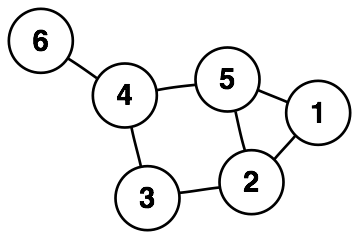
In this graph, node 4 is connected to nodes 3, 5, and 6. Our graph dictionary would then have the following key: value pair:
graph[4] = {3, 5, 6}
We would have similar key: value pairs for each one of the nodes in the graph.
Shortest path function input and output
Function input
Our BFS function will take a graph dictionary, and two node ids (node1 and node2). For this tutorial, each graph will be identified using integer numbers (1, 2, etc).
Function output
The function will return a list of nodes that connect node1 and node2, starting with node1 and including node2: [node1, node_x, node_y, ..., node2]. This list will be the shortest path between node1 and node2.
If there is more than one possible shortest path, it will return any of them.
In case no path is found, it will return an empty list [].
from typing import Dict, List
def shortest_path(graph: Dict[int, set], node1: int, node2: int) -> List[int]:
pass
Shortest path algorithm
Our algorithm starts by defining a list of possible paths. A “path” is a list of connected nodes. Initially, we have only one “path” possible: [node1], because we start traversing the graph from that node. We also define a set of previously visited nodes to avoid backtracking.
After these initial steps the algorithm does the following:
- Take the next path from the list of paths.
- If all possible paths have been traversed, stop. No path was found.
- Set the “current node” to the last node in the current path.
- Search the goal node,
node2, between the nodes that are connected to the current node.- If node2 is connected to the current node, we have found path from node1 to node2. Stop.
- If node2 isn’t connected to the current node, update the list of paths to traverse.
- Add a new path from
node1to each one of the connected nodes to traverse next.
- Add a new path from
- Go back to step 1.
Shortest path implementation in Python
Finally, we have the implementation of the shortest path algorithm in Python.
def shortest_path(graph, node1, node2):
path_list = [[node1]]
path_index = 0
# To keep track of previously visited nodes
previous_nodes = {node1}
if node1 == node2:
return path_list[0]
while path_index < len(path_list):
current_path = path_list[path_index]
last_node = current_path[-1]
next_nodes = graph[last_node]
# Search goal node
if node2 in next_nodes:
current_path.append(node2)
return current_path
# Add new paths
for next_node in next_nodes:
if not next_node in previous_nodes:
new_path = current_path[:]
new_path.append(next_node)
path_list.append(new_path)
# To avoid backtracking
previous_nodes.add(next_node)
# Continue to next path in list
path_index += 1
# No path is found
return []
We return the trivial path [node1] for the case node1 == node2.
Variable path_index keeps track of the path that we’re currently following. We stop the loop when we reach the end of path_list.
At all times, we have a shortest path from node1 to last_node. Based on this path, we can find the path from node1 to node2 if node2 is connected to last_node.
The order in which new paths are added to path_list guarantees that we traverse the graph in breadth first order.
Verification
Let’s check our algorithm with the graph shared at the beginning of this post.

We create a graph dictionary.
graph = {}
graph[1] = {2, 5}
graph[2] = {1, 3, 5}
graph[3] = {2, 4}
graph[4] = {3, 5, 6}
graph[5] = {1, 2, 4}
graph[6] = {4}
Now, let’s find the shortest path from node 1 to node 6.
>>> shortest_path(graph, 1, 6) [1, 5, 4, 6]