In this post, we’ll see how to convert a float to an int in C. We’ll assume both int and float datatypes to be 32-bits long an int using two’s complement representation for negative values. The conversion will be performed using the bit-level representation of the float data type. Only addition, subtraction, and bitwise operations will be used.
To convert from int to float, you can see this post.
This is also a solution for exercise 2.96 of the Computer Systems: A Programmer’s Perspective book.
Rounding to whole numbers
Before we begin, let’s study how C will handle rounding from float to int. The rounding mode used is round towards zero.
For positive values, we round down:
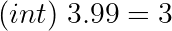
Negative values are rounded up:
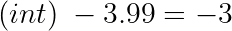
In practical terms, the fractionary part is truncated.
Getting the floating-point fields
The floating-point single-precision data representation (float), consists of three different fields.
These fields are used to encode a number in the form:
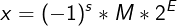
- One bit encodes the sign:
s. - 8 bits encode the exponent, E. We’ll call this bits
exp(in green on the image above). - 23 bits encode the magnificand, M. We’ll call them
fracbits (in red on the image above).
For our converter, we’ll start by getting these different fields.
unsigned s = f >> 31; unsigned exp = f >> 23 & 0xFF; unsigned frac = f & 0x7FFFFF;
They are obtained by shifting operations combined with masks to get the necessary bits. On the code snippet above, f contains the 32-bit float representation of the value.
Special cases: NaN and Infinity
Floating-point encodes special values such as NaN (not a number, obtained by expressions such assqrt(-1) or 0.0 / 0.0) and infinity (for values that overflow) with the exp field all set to ones. For these special cases, we’ll return the special value 0x80000000 (which corresponds to INT_MIN).
if (exp == 0xFF) return 0x80000000;
A value preceded by 0x, such as 0xFF , is used to denote an hexadecimal number.
Denormalized values
Denormalized values are those in which the exp field is all zeros. In floating-point representation, they are used to encode values that are very close to zero (both positive and negative). All of these values will be rounded to zero.
if (exp == 0)
return 0;
Normalized values
Finally, we can focus on normalized values. In this case, the exp field is neither all ones nor all zeros. For this group of values, the exponent E is encoded as:
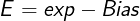
Where exp is the unsigned 8-bit number represented by the exp field and Bias = 127. We can get the exponent E as follows:
int E = exp - BIAS;
Values less than one
First, let’s consider values that are in the range -1 to 1 (not including -1 and 1). All of these values will be rounded to zero. Positive values will be rounded down, and negative values will be rounded up. In both cases, the result will be 0. These cases will take place when the exponent E is less than 0:
if (E < 0) return 0;
For instance, if E = -1, the encoded float will be a binary fraction in the form:
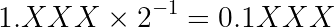
Where XXX represents the fractionary part of the magnificand, encoded by the fracfield. 0.1XXX is a binary fraction less than one.
Overflowing
The range of int values is between INT_MIN = -2^31 = 2147483648 and INT_MAX = 2^31 - 1 = 2147483647. For float values beyond that range, we’ll return 0x80000000 as a way of encoding overflow.
The int datatype represents numbers using 31 bits (the remaining bit is used for the sign). This means that the binary representation of our value can be at most 31 bits long. This limit case will take place when E = 30:
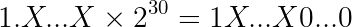
X...X are the 23 bits of the frac field. The value 1X...X0...0 will be 31 bits long: a leading one + 23 frac bits + 7 zeros.
We can conclude that float will overflow when E > 30:
if (E > 30) return 0x80000000;
Normalized values in the range of int
Finally, we’re left with the float values that can be rounded to an int other than zero and that won’t overflow.
The frac field is 23 bits long. Remember that the exponent E and frac encode a value in the form:
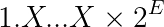
Where each X is one of the 23 binary digits of the frac field. They represent the digits that come after the binary point (fractionary part).
A positive value of E will shift the binary point E places to the right. For instance if E = 2:
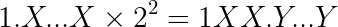
Here we’re using the symbol Y for the 21 frac binary digits that come after the binary point.
As it was mentioned above, when we cast a float to int, C will truncate the fractionary part.
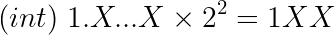
That means that the rightmost 23 - 2 = 21 bits of the frac field are discarded.
On the other hand, if E is larger than 23, the binary point will be shifted beyond the bits of the frac field and we’ll have extra zeros to the right:
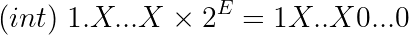
We will have E - 23 trailing zeros.
These conditions can be fulfilled by the appropriate shifting operations. We shift frac to the right (>>) in order to discard the least significant bits when E < 23, and we shift to the left (<<) to add trailing zeros.
int x = 1 << E; if (E < 23) x |= frac >> (23 - E); else x |= frac << (E - 23);
Here x is the resulting bit-level int representation. First, we shift the leading one E places to the left. Then, we get the integer part of the float value by shifting operations as it was mentioned above. Note that we use the bitwise OR operator (|) as a way of “adding” the leading one and the lower order bits of the frac field (e.g. 100 | 001 = 101 ).
Negative values
Finally, we modify the bit encoding for negative values.
if (s == 1) x = ~x + 1;
The expression ~x+1 is just a binary operation that yields -x in two’s complement representation.
Complete program and testing
Putting all of the pieces together in the float_f2i function, we get:
#define NAN 0x80000000
#define BIAS 127
#define K 8
#define N 23
typedef unsigned float_bits;
/* Compute (int) f.
* If conversion causes overflow or f is NaN, return 0x80000000
*/
int float_f2i(float_bits f) {
unsigned s = f >> (K + N);
unsigned exp = f >> N & 0xFF;
unsigned frac = f & 0x7FFFFF;
/* Denormalized values round to 0 */
if (exp == 0)
return 0;
/* f is NaN */
if (exp == 0xFF)
return NAN;
/* Normalized values */
int x;
int E = exp - BIAS;
/* Normalized value less than 0, return 0 */
if (E < 0)
return 0;
/* Overflow condition */
if (E > 30)
return NAN;
x = 1 << E;
if (E < N)
x |= frac >> (N - E);
else
x |= frac << (E - N);
/* Negative values */
if (s == 1)
x = ~x + 1;
return x;
}
In order to handle the bit-level representation of float values with bitwise operators, we use the unsigned datatype which we call float_bits. Additionally, we wrote some of the numerical constants as K = 8 for the length of the exp field and N = 23 for the length of the exp field.
Testing
The program was tested as follows:
#include <limits.h>
#include <assert.h>
typedef unsigned float_bits;
int float_f2i(float_bits f);
int main() {
int bits;
float *fp;
float_bits *fbp;
for (bits = INT_MIN; bits < INT_MAX; bits++) {
fp = &bits;
fbp = &bits;
assert((int) *fp == float_f2i(*fbp));
}
return 0;
}
We used the variable bits to generate all the possible bit-level combinations. The address of bitswas then referenced as datatypes float and float_bits to perform the test. Finally, we verified that the result of casting float to int was the same as the return value of the float_f2i function.
When compiled, we received no error output which means that the converter worked for all of the tested values.

Hey, great post, helped me a lot, thanks!! 🙂
You’re welcome!
This is the single best page explaining this operation, thank you! I’m building a bare-metal system that uses floats. In my tiny float-printing code, there in an innocuous-looking cast of the float to int:
whole = (int)value.f;
That’s fine for a C compiler, don’t even have to really think about it. But implementing it on bare metal where there are NO standard libraries or even a compiler — that’s a harder problem.
Thank you! — JH
Glad this helped you, Joe. If you want to take a closer look at bit-level manipulation, I highly recommend Chapter 2 of CS:APP.