A heap is a tree data structure where each child node is greater than its parent node.
child node >= parent node
With this property satisfied, it’s ensured that the root node is the minimum value in the heap. This is very useful for many types of problems. Getting the minimum value in the heap is O(1), and both adding new values and removing the root node are O(log n).
To be more precise, the description above corresponds to a min heap. Similarly, if each child node is smaller than its parent node, we have a max heap. In general, nodes can be compared using any criterion, depending on the properties of the nodes. We’ll focus on min heaps in this blog post, but the principles can be generalized to any kind of heap.
Heap properties and uses
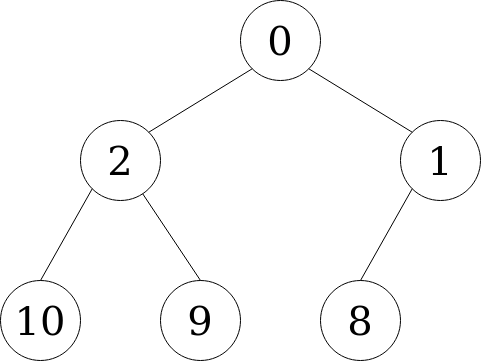
A heap allows us to recover the smallest element in a collection in constant time O(1). Consider the heap below.
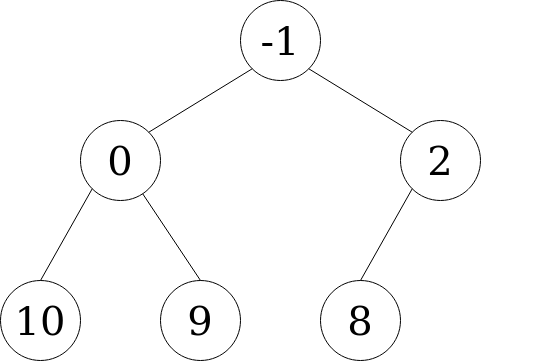
It consists of 6 nodes, with the (unordered) values: [2, 10, -1, 9, 0, 8]. See that the value at the top, -1, is the minimum in the collection. Getting the minimum of a heap is as simple as getting the root node.
There is only one condition that holds in the heap: each child is greater than its parent. There is no ordering between children nodes at the same level. This simple single condition allows for efficient ordering of the elements.
Heaps allow for two extra operations: deleting the root node (which is always the minimum value) and adding any new value. Both operations are performed in logarithmic time O(log n).
Adding new elements
Every time we add a new element, we fill the next available position in the tree, from top to bottom, left to right. Let’s add the value 1. It would fill the empty right child of node 2.
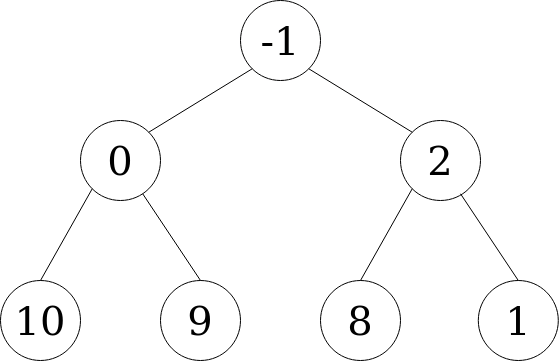
After adding this new node, the heap isn’t ordered. We have to reestablish the property of each child node being greater than its parent. This can be done by “bubbling up” the new node 1 until it’s greater than its parent node. We do this by swapping positions between the new node and its parent.
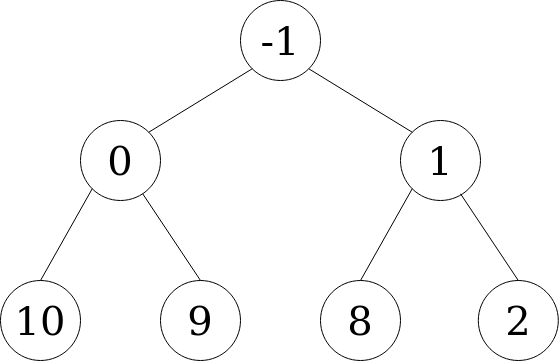
Then, we compare node 1 with its new parent, and continue bubbling up the node if the heap property still isn’t satisfied or until we have reached the root node. In this case, 1 is greater than its parent -1, so we stop. If we had added a value such as -2, it would have bubbled up all the way up to the root node. This bubbling up process is performed in O(log n). Once we’re done, the root node is once again the minimum in the collection.
Deleting values
Deletion is possible only for the root (minimum) node. It’s performed by removing the root node and substituting it with the last node (from top to bottom, left to right).
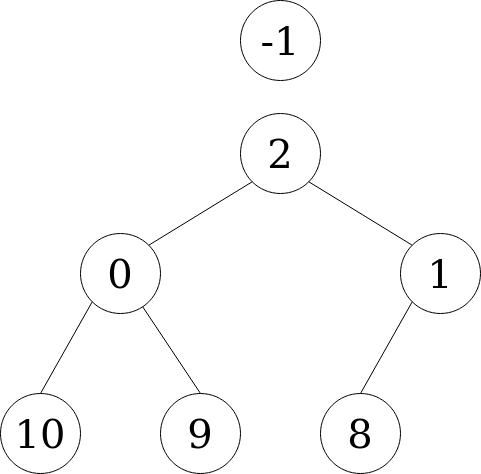
See that node -1 isn’t part of the heap anymore. See also that the heap property (each child is greater than its parent) isn’t satisfied anymore. We have to “sink down” the new root node to its correct position. This is done by swapping the position of the parent node with the smallest of its children. We start by swapping 2 and 0.
This process continues as long as the heap property isn’t satisfied or until we reach the bottom of the tree. In this case, the heap is ordered again after swapping nodes 2 and 0, so we stop. After reordering, the root node of the heap is again the smallest in the collection. This reordering process after deletion is also O(log n).
Heap tree data structure implementation
We could implement the heap using node objects.
class Node {
constructor(val, left, right) {
this.val = val;
this.left = left ? left : null;
this.right = right ? right: null;
}
}
However, an easier and more efficient approach is to just use an array. We stack the elements of the heap, from top to bottom, left to right.
For our initial heap example:

This would result in the array:
[-1, 0, 2, 10, 9, 8]
In order to simplify the indices of the heap nodes in the array, we add a dummy value at the beginning of the array.
[-1, -1, 0, 2, 10, 9, 8]
We used the value -1, but null or any other value works fine, too.
Counting the nodes starting from 1, yields the following result:
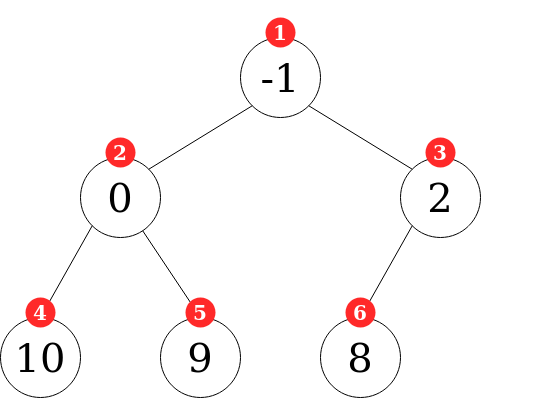
See that with this convention, we can get the parent, left node, and right node for any node at index i as follows:
parent index = Math.floor(i/2)
left index = 2*i
right index = 2*i + 1
For example, the left child of node at index3 is 2 * 3 = 6. Its parent node is 3 / 2 = 1.
Heap implementation
As it was stated, we will use an array to store the heap’s tree. The first value of the array is a dummy value, -1.
class MinHeap {
constructor(values) {
this.list = [-1];
if (typeof values == "number") values = [values];
values.forEach((value) => this.add(value));
}
...
}
The heap is constructed by passing an array of numbers (or a single number that is converted to an array), to it. Then, each value is added to the heap using the add method.
class MinHeap {
...
add(value) {
const len = this.list.length;
// add value to heap
this.list.push(value);
if (len == 1) {
return value;
}
// reorder from bottom to top
this.heapifyUp();
return this.list[1];
}
}
Adding a value to the heap starts by adding it to the next empty position in the tree. This is as simple as callingthis.list.push. If the heap has only one value, it’s already ordered. Otherwise, we call the heapifyUp method to reorder the heap. Once that’s done, this method returns the minimum value in the collection, which is the one with index 1.
Removing elements is done by taking the bottom-right node of the tree and moving it to the root. Prior to that, we verify the heap is not empty. We also deal with the trivial case of a heap with a single element. After replacing the root node with the last node, we reorder the heap with the heapifyDown method. The deleted element, which corresponds to the previous minimum value, is returned.
class MinHeap {
...
remove() {
if (this.list.length == 1) return null;
if (this.list.length == 2) return this.list.pop();
const prevRoot = this.list[1];
// bring last val to root
this.list[1] = this.list.pop();
// reorder top to bottom
this.heapifyDown();
return prevRoot;
}
}
The reordering functions are implemented as follows:
When we add a new node, it will always be the last value in the array.
- Compare the new node with its parent node.
- If the new node is smaller than its parent, the heap is not ordered. Parent and new node swap positions.
- Repeat from 1 until reaching the root node or 2 is false.
class MinHeap {
...
heapifyUp() {
let i = this.list.length - 1;
const val = this.list[i];
while (!this.isRoot(i) && this.getParentNode(i) > val) {
// swap values
[this.list[this.getParentIndex(i)], this.list[i]] = [
val,
this.getParentNode(i),
];
i = this.getParentIndex(i);
}
}
}
When we remove the root node, the last node of the tree takes its place.
- Start from the new root node, with value
val. - If node
valis greater than any of its children, replace it with the smallest child. - Else stop.
- Repeat from 2 until it’s false or reaching the bottom of the tree.
class MinHeap {
...
heapifyDown() {
if (this.list.length < 3) return;
let i = 1;
const currentVal = this.list[1];
let leftVal = this.getLeftNode(i);
let rightVal = this.getRightNode(i);
while (
leftVal !== undefined &&
(currentVal > leftVal || currentVal > rightVal)
) {
if (
currentVal > leftVal &&
(rightVal === undefined || leftVal < rightVal)
) {
[this.list[this.getLeftIndex(i)], this.list[i]] = [currentVal, leftVal];
i = this.getLeftIndex(i);
} else {
[this.list[this.getRightIndex(i)], this.list[i]] = [
currentVal,
rightVal,
];
i = this.getRightIndex(i);
}
leftVal = this.getLeftNode(i);
rightVal = this.getRightNode(i);
}
}
}
We add special clauses to deal with empty nodes, which yield undefined.
All of the above functions use the following helpers:
class MinHeap {
...
isRoot(index) {
return index == 1;
}
getLeftIndex(index) {
return 2 * index;
}
getLeftNode(index) {
return this.list[this.getLeftIndex(index)];
}
getRightIndex(index) {
return 2 * index + 1;
}
getRightNode(index) {
return this.list[this.getRightIndex(index)];
}
getParentIndex(index) {
return Math.floor(index / 2);
}
getParentNode(index) {
return this.list[this.getParentIndex(index)];
}
}
Example
Let’s use the heap to get the minimum value of the array: [1, 2, 3, -10, -100, 99, 0].
const heap = new MinHeap([1, 2, 3, -10, -100, 99, 0]) heap.remove() // -100 heap.remove() // -10 heap.add(-3) // -3 heap.add(5) // -3
Bonus: Implementing heapsort
After every removal, the heap reorders itself so that the minimum value is always at the root. This means that subsequent calls to the remove method will yield the heap values in increasing order. We’ll exploit this to implement a sort algorithm.
class MinHeap {
...
sort() {
const sorted = [];
let nextVal;
while ((nextVal = this.remove()) !== null) {
sorted.push(nextVal);
}
return sorted;
}
}
Let’s see it in action.
const heap = new MinHeap([1, 2, 3, -10, -100, 99, 0]) heap.sort() // [ -100, -10, 0, 1, 2, 3, 99 ]
Since reordering the heap after each removal is O(log n) sorting an array of n elements with heapsort is O(n log n). Quite performant!
Additional resources
- Videos explaining heaps: freeCodeCamp, hackerRank
- Heap implementation explanation: Wikipedia.
- Codepen with demo and TypeScript source code: codepen.