Converting int to float in C

In this post, we’ll see how to manipulate an integer value to get its single-precision floating-point bit representation. Specifically, we’ll convert an int data type to a float data type in C assuming a word size of 32 bits. An example can be seen below.

Most of the work will be done using bit-level operations, addition, and subtraction. We’ll help ourselves with the log function at one point, though.

As a first approach, this “converter” will not handle rounding effects. This means that it will yield the same results as casting int to float only in the range -10M to +10M. Larger values need to be rounded due to the limited precision of floating-point. This converter won’t handle those cases. For a converter that handles rounding effects as well, see this post.

The IEEE single-precision floating-point

Floating-point representation approximates a real value x as:

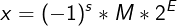
Each of these variables is encoded with a field of bits. For single-precision floating-point (32 bits), we have:

• The sign field s with 1 bit.
• The magnificand M with 23 bits.
• The exponent E with 8 bits.

The sign field is just encoded to 0 for positive values and 1 for negative ones.

The magnificand M is a binary fraction in the form:

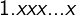
Where each x is a binary digit, 0 or 1. For whole numbers such as integers, the range of floating-point values are said to be normalized. In this case, we encode only the bits following the binary point (a leading 1 is implied). The precision of the fractionary part xxx...x is limited to 23 bits. This is known as the frac field.

Finally, we have the exponent field. The value of E is linked to the 8 bits used to encode it as follows:

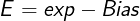
Where exp is an unsigned 8-bits value (range 0-255) and Bias = 127. The possible range of E values is between -126 to 127 (the exponent field can’t be all zeros or all ones for normalized values).

These three fields together form the 32 bit single-precision floating-point bit representation of a number as follows:

With s being 1 bit, exp 8 bits and frac 23 bits long.

Floating-point encoding example

As an example, let’s see how is the number 24800 encoded in floating-point representation.

Since it’s a positive value, we’ll have s=0.

To decode the values of M and E we’ll transform 24800 to a binary value:

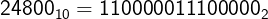
Now, we’ll express this binary value in the form M * 2^E:

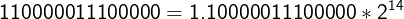
We get E=14 which means that exp = E + Bias = 141. The value 141 (in decimals) needs to be encoded as an unsigned 8-bit number: exp = 10001101.

We also get M=1.10000011100000. The digits after the binary point are 10000011100000. These are encoded in the frac field. We pad to the right with zeros (they don’t change the binary fraction value) to get 23 bits:

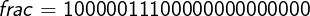
Finally, we’ll get the following 32-bit encoding for the number 24800 as a single-precision floating-point:

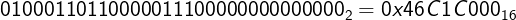
Integer to floating-point converter

Now, we’ll see how to program the converter in C. The steps that we’ll follow are pretty much those of the example above. We’ll assume int encodes a signed number in two’s complement representation using 32 bits.

We’ll reproduce the floating-point bit representation using theunsiged data type. We’ll call this data type float_bits.

typedef unsigned float_bits;

First, we’ll determine the sign bit s. The value we are converting to a float is int i.

unsigned s = i>>31;

To get s, we’re just shifting to the leftmost bit of the 32 bit integer. In two’s complement representation, this value is 1 for negative values and 0 for positive ones, just like for floats.

Next, we’ll get the exponent.

unsigned E = (int) (log(i<0 ? -i : i)/log(2));
unsigned exp = E + 127;

With the first line, we get the highest power of two E such that i >= 2^E. We do that with the logarithm base 2 operator:

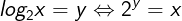
With the second line, we account for the Bias = 127 to get exp.

Finally, we’ll calculate the frac field. We start by calculating M. We can drop the negative sign and deal only with the absolute value of i since the sign is already encoded by s:

unsigned M= i>0 ? i : -i;

The frac field is obtained by dropping the most siginificant 1:

unsigned frac = M ^ (1<<E);

At this point, frac contains all of the bits after the leading one.

Next, we push the start of the frac field to the 23th bit position:

  if (E>=23)
    frac >>= E-23;
  else
    frac <<= 23-E;

The frac field is 23 bits long. The exponent E says how many of these places are already used. We truncate to only the most significant 23 bits if the field is too long or pad with zeros to the right if the field is too short.

See that what we do for large numbers is to truncate. This is equivalent to rounding towards zero. The default C behavior is to round-to-even (it will round to the closest value). For this reason, the result of our converter will differ from C’s casting for large values (those with more than 24 significant bits) .

Finally, we accommodate all of the fields together:

s<<31 | exp<<23 | frac;

Putting it all together in the float_i2f function, we’ll get:

float_bits float_i2f(int i) {
  /* Special case : 0 is not a normalized value */
   if (i==0)
    return 0;

  /* sign bit */
  unsigned s = i>>31;

  /* Exponent */
  unsigned E = (int) (log(i<0 ? -i : i)/log(2));
  unsigned exp = E + 127;

  /* Magnificand*/
  unsigned M= i>0? i : -i;
  unsigned frac = M ^ (1<<E);
      
  /* Move frac to start at bit postion 23 */
  if (E>=23)
    /* Too long: Truncate to first 23 bits */
    frac >>= E-23;
  else
    /* Too short: Pad to the right with zeros */
    frac <<= 23-E;
  
  return s<<31 | exp<<23 | frac;
}

We included a special clause for i=0 that is not a normalized value.

Testing

To test the validity of our converter, we’ll compare the results of the float_i2f function with the casting operation (float) i.

int main() {
  int i;
  float *fp; 
  float_bits f;
  
  for (i=-1e7; i<1e7; i++) {
    f = float_i2f(i);
    fp = &f;
    if (*fp != (float) i)
      printf("Casting not equal for value: %d\nConverted value is %.0f\nCasted value is %.0f\n", i, *fp, (float) i);
  }
}

Under the hood, the float_bits data type is just the unsigned data type. In order to make C recognize those bits as a float, we declare a float pointer float *fp and pass it the address of the float_bits result: &f. This way, the bits at *fp will be recognized as floats by C.

After compiling and running this code, we’ll get no output. This means that the values of the converter and the casting operation were all equal for the tested range of integer values. For a converter that handles the whole range of int values, you can this post.