The Memory Mountain is a graphical representation of the read bandwidth (the rate data is read by a program in MB/s) in terms of the total data size processed and its access pattern. It provides great insight into the way CPU cache helps bridge the gap between the high-speed processor and the relatively slow access times of the main memory. It was introduced by Stricker and Gross, and I first read about it in Computer Systems: A Programmer’s Perspective (CS:APP).
In this post, we’ll generate a memory mountain with the diagnostic program provided by CS:APP and plot it using Python’s matplotlib. Then we’ll analyze it to gain some insight about the memory hierarchy. In particular, we’ll estimate the CPU cache sizes.
Measuring the memory read bandwidth
As it was mentioned, the program used to measure the read bandwidth is the one provided by CS:APP. You can get it from their website (file mountain.tar in the Chapter 6 section).
Data
The program allocates 128 MB of memory for an array of long elements (long is usually 8 bytes).
#define MAXELEMS (1 << 27)/sizeof(long) long data[MAXELEMS];
It then proceeds to initialize the array with each element as data[i] = i.
for (int i = 0; i < n; i++) data[i] = i;
Testing memory access
The actual operation that is measured, is the test function. This function iterates over some elements of the array to calculate their total sum. In order to take advantage of modern processors parallelism, this operation is performed by 4 accumulators simultaneously.
int test(int elems, int stride) {
...
for (long i = 0; i < elems; i += sx4) {
acc0 = acc0 + data[i];
acc1 = acc1 + data[i+stride];
acc2 = acc2 + data[i+sx2];
acc3 = acc3 + data[i+sx3];
}
...
return ((acc0 + acc1) + (acc2 + acc3));
}
A couple of parameters come into play here: the number of elements elems, and the stride.
The first one, elems, is derived from the portion of the array that is processed expressed by the variable size in bytes.
int elems = size / sizeof(long);
size values correspond to 16KB, 32 KB, 128 KB, 256 KB, 512 KB, 1 MB, 2 MB, 4 MB, … up to 128 MB.
The stride defines the access pattern. The simplest one is stride=1, which corresponds to sequential access: we access the array elements in the order i, i + 1, i + 2, etc. In general, a stride-k access pattern would access the array elements in the order: i, i + k, i + 2k, etc.
stride takes values between 1 and 15.
The other variables in the code snippet, sx2, sx3, and sx4, are just multiples of stride used to process the multiple sum accumulators (acc0 to acc3) in parallel.
Measuring performance
The fcyc2 function measures the CPU cycles it takes test to run. With this information, as well as the processor’s clock rate (obtained from /proc/cpuinfo, variable Mhz), it returns the read bandwidth as:
double run(int size, int stride, double Mhz) {
...
cycles = fcyc2(test, elems, stride, 0);
return (size / stride) / (cycles / Mhz); // MB/s
}
size / stride is a value in bytes. cycles / Mhz is a time in microseconds. The final result is the read bandwidth in MB / s.
The read bandwidth is calculated for every combination of size and stride.
Running the memory mountain program
Executing mountain yields the following table.
$ ./mountain Clock frequency is approx. 2030.5 MHz Memory mountain (MB/sec) s1 s2 s3 s4 s5 s6 s7 s8 s9 s10 s11 s12 s13 s14 s15 128m 5412 2849 1984 1523 1243 1039 897 780 702 637 595 545 511 487 461 64m 5509 2892 2007 1525 1254 1056 900 769 709 643 593 542 510 492 470 32m 5538 2856 2001 1575 1262 1059 901 791 708 638 594 548 517 492 465 16m 5483 2897 1998 1574 1276 1037 911 793 712 646 595 549 519 492 474 8m 6704 3575 2486 1934 1599 1331 1147 997 910 847 786 741 720 707 715 4m 12623 8458 6679 5319 4406 3732 3228 2842 2839 2871 2902 2962 3042 3080 3164 2m 14230 10136 8697 6890 5616 4701 4052 3547 3544 3522 3521 3524 3508 3506 3512 1024k 14360 10248 8939 7052 5699 4761 4113 3586 3584 3552 3541 3534 3531 3518 3512 512k 14347 10435 8950 7023 5695 4785 4130 3585 3583 3590 3637 3747 3750 3919 4104 256k 14948 12462 11642 9075 7676 6656 5874 5060 6136 6396 6434 6516 7013 7092 7491 128k 15354 13997 13621 12659 11529 10204 9065 8300 8888 8732 8804 8606 8394 8728 8723 64k 15499 14046 13454 12573 11506 10031 8912 8704 8646 8530 8524 8439 8509 8657 11201 32k 16344 16142 15932 15619 15401 15274 15842 13016 14408 15187 15270 14214 12824 14942 14078 16k 16626 15933 16001 14825 14782 15659 14530 11848 12832 14982 13089 11131 12729 10420 13198
The final step is to plot the results.
Graphing the memory mountain
We’ll graph the ./mountain results we got above with the following script (graph.py).
#!/usr/bin/env python3
import sys
import numpy as np
import matplotlib.pyplot as plt
def main():
x = np.arange(1, 16) # stride
y = np.arange(1, 15) # size ticks
x, y = np.meshgrid(x, y)
xticks = list((map(lambda stride: "s" + str(stride), range(1, 16))))
yticks = "128m 64m 32m 16m 8m 4m 2m 1024k 512k 256k 128k 64k 32k 16k".split()
z0 = sys.argv[1]
z1 = z0.splitlines()[3:]
# Divide by tab, discard first and last column
z2 = np.array(list(map(lambda line: line.split("\t")[1:-1], z1)))
z2 = z2.astype(np.int)
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.set_xticks(range(1, 16, 2))
ax.set_yticks(range(1, 15, 2))
# Take only every other label
plt.rcParams.update({"font.size": 16})
ax.set_xticklabels(xticks[::2])
ax.set_yticklabels(yticks[::2])
ax.tick_params(axis="z", pad=10)
ax.set_xlabel("Stride", fontsize=18, labelpad=20)
ax.set_ylabel("Size", fontsize=18, labelpad=20)
ax.set_title("Memory Mountain\n", fontsize=22)
ax.plot_surface(x, y, z2, cmap="jet")
plt.tight_layout()
plt.show()
We can execute it as follows:
$ ./graph.py "$(./mountain)"
"$(./mountain)" will evaluate it and pass the results as an argument to graph.py.
Analyzing the memory mountain
We’ll get a window with the following graph (the black dashed lines were added by me).
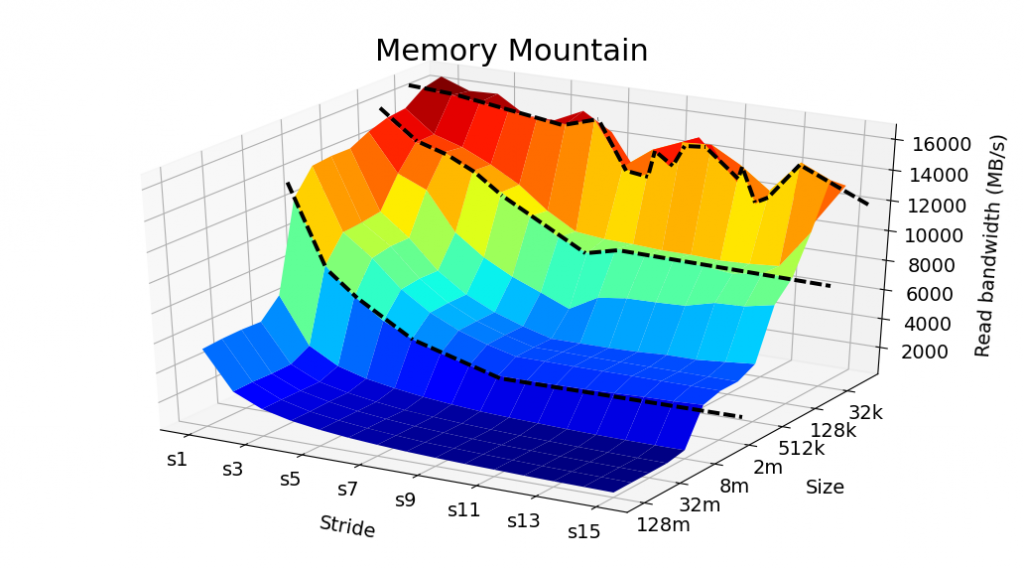
There are many interesting results that can be noted. The black dashed lines show the “size limits” for which we have sharp decreases in the bandwidth for any given stride. For example, as we increase the size from 32 KB, top black dashed line, to 64 KB, the bandwidth dramatically decreases. These limits are indicators of the CPU cache sizes.
The top dashed line corresponds to the L1 cache. It’s the fastest one (thus explaining the greatest read bandwidths), but also very limited in size. Based on the graph, we estimate it to be 32 KB. Next, we have the L2 cache. It’s a bit slower than L1, but larger in size. We estimate it to be 128 KB. Finally, we have the L3 cache. The graph suggests it has a size of 4 MB.
A side-view of the plot helps visualize the cache sizes.
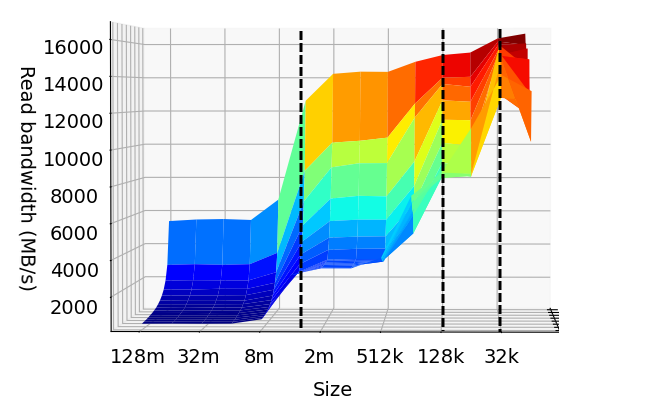
The blue zone with the least read bandwidth, corresponds to the main memory (RAM). The CPU cache is unable to store all of the data for sizes larger than 8 MB (given my system’s hardware). Then, the CPU is required to constantly fetch the information from the main memory. This process is relatively slow and dramatically decreases the read bandwidth.
Spatial locality
A second important result can be seen with the decrease in bandwidth as the stride increases for any given data size. The largest bandwidth, for any size, is obtained through sequential access (stride-1). A more detailed analysis of the effect of spatial locality can be seen in my previous post about array reference performance.
Estimated vs. actual CPU cache sizes
My processor is an Intel Core i5. Its CPU cache specifications correspond pretty well with the results of the memory mountain.
| CPU Cache | Size |
| L1 | 32 KB |
| L2 | 256 KB |
| L3 | 6 MB |
The largest divergence was in the L2 cache size. See that for a size of 256 KB, we get read bandwidths that are in-between a sharp decrease between 128 KB and 512 KB. This could be because the L2 cache is required to store other data besides the array values, being then used beyond its capacity when we test it with an array of 256 KB.
In conclusion
It’s quite amazing to see the effect of low-level hardware on program performance. The most important aspect, however, is what we can learn to write better programs. First, writing programs that process data, as much as possible, in sequential access to exploit spatial locality. And secondly, reduce the size of the working data set that is being processed at a given time to exploit temporal locality.