In this post, we’ll program an int to float converter that will handle the whole range of int values . We’ll base our work on the results of the previous converter which didn’t handle rounding effects.
This is also a solution for exercise 2.97 of the Computer Systems: A Programmer’s Perspective book.
The initial converter
We’ll start working with the following implementation of the converter:
/* Convert 32-bits int to float */
float_bits float_i2f(int i) {
/* Special case : 0 is not a normalized value */
if (i==0)
return 0;
/* sign bit */
unsigned s = i>>31;
/* Exponent */
unsigned E = (int) (log(i<0 ? -i : i)/log(2));
unsigned exp = E + 127;
/* Magnificand*/
unsigned M= i>0 ? i : -i;
unsigned frac = M ^ (1<<E);
/* Move frac to start at bit postion 23 */
if (E>23)
/* Too long: Truncate to first 23 bits */
frac >>= E-23;
else
/* Too short: Pad to the right with zeros */
frac <<= 23-E;
return s<<31 | exp<<23 | frac;
}
The details of which we covered in this post.
First of all, let’s see which cases aren’t correctly handled.
Understanding rounding effects (round-to-even)
Single-precision floating-point has a limited precision of 23 bits for its frac field. Numbers that require more than 23 bits for their fraction part when encoded as floats will have to be rounded.
For example, let’s take the number 123456789 (in decimals). Converting to binary, we’ll have:
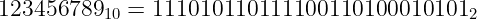
And expressing it as a binary fraction:
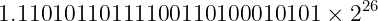
As it can be seen, there are 26 significant digits after the binary point. Since the frac field can only accommodate for 23 of them, we won’t be able to exactly express this value. It will have to be rounded.
C handles rounding with the round-to-even mode. In this mode, we round to the closest possible value. See that for 123456789 in binary, we’ll round-off the last 3 digits: 101. Since the highest order bit of 101 is 1, we’ll add one to the least significant digit of the rounded value:
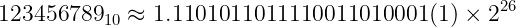
See that the new binary fraction is only 23 digits long after the binary point. The last digit was enclosed in parenthesis for clarity. If we had merely truncated to the 23rd digit after the binary point, it would have been 0. Because of rounding, we added 1 to it.
This is how C would handle most rounding cases. There’s only one special case.
When the value is equally distant to two possible rounded values, C will choose the value that ends with an even least significant digit. For example, if we were rounding 2.5 (in decimals) to a whole number, we can see that it’s equally distant from both 2 and 3. In round-to-even mode, 2 is chosen because it’s even.
With binary numbers, we have this case whenever the rounded-off digits are in the form 10...0 (a one followed by zeros). That’s the case for 123456788:
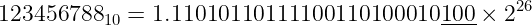
We have underlined the digits that will be rounded-off (100 ) to accommodate to 23 digits after the binary point. See that it’s a 1 followed by zeros. In this case, the value is equally distant from 1.11010110111100110100010 * 2^26 and from 1.1101011011110011010001 * 2^26 , the two possible rounding options. C will choose the first option (the one that ends with 0), because it’s even.
Finally, the rounded binary fraction will be:
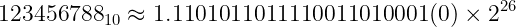
Just like before, the rounded digit was enclosed in parentheses for clarity.
Now, we’ll see how to implement these changes in the converter.
Converter: rounding to the closest value
First of all, we’ll make the converter round to the closest value. As it was seen in the previous section, we just need to check the 24th digit of the binary fraction. If it’s 0, we leave the rounded digit as it is. If the 24th binary digit of the fraction is 1, we add 1 to the rounded digit.
All of the changes will take place only when the frac field is more than 23 digits long. We’ll accommodate the changes in the correspoding section of the code.
if (E>23) {
/* Frac field too long */
unsigned round = frac >> (E - 24) & 1;
frac >>= E-23;
frac += round;
}
The first code line after if gets the 24th digit of the frac field. It will be either 0 or 1. After shifting the frac field, we increment it by the value of round.
Testing
We’ll test this new implementation in the range of values 100000000 to 100000020. These values require more than 23 digits in the frac field, so rounding will be required.
int main() {
int i;
float *fp;
float_bits f;
for (i=1e8; i<1e8+20; i++) {
f = float_i2f(i);
fp = &f;
if (*fp != (float) i)
printf("Casting not equal for value: %d\nConverted value is %.0f\nCasted value is %.0f\n", i, *fp, (float) i);
}
}
After compiling and executing, we get:
$ gcc i2f_roundv1.c -lm -o main $ ./main Casting not equal for value: 100000004 Converted value is 100000008 Casted value is 100000000
Here we can see that the converter is adequately handling most rounding cases. The only value it didn’t handle correctly was 100000004. Its binary representation is:
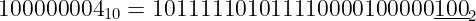
The digits that need to be rounded-off have been underlined. We can see this is a case where the two rounding options are equally distant. 100000004 is equally distant from 100000000 and from 100000008.
To adequately handle this cases, we’ll need to add a round-to-even feature to our converter.
Converter: round-to-even
We have to implement a special case when the rounded-off digits are in the form: 10...0 (a one followed by zeros). In that case, if the last frac digit is 0, we leave it unchanged. If the last frac digit is 1, we round the least significant digit by adding 1 to it.
We can implement those changes as follows:
/* Round to closest */ unsigned round = frac >> (E - 24) & 1; /* Rouund-to-even modification */ unsigned last_frac_bit = frac >> (E - 23) & 1; unsigned rounded_off_digits = frac << 32 - E + 23 >> 32 - E + 23; unsigned one_followed_by_zeros = 1 << E - 24; if (rounded_off_digits == one_followed_by_zeros) round = last_frac_bit; frac >>= E-23; frac += round;
rounded_off_digits will get the bits of the frac field after the 23rd digit. We do so by setting all of the bits that come before to 0 with shift operations. We compare them with a value of the form 10...0 (one_followed_by_zeros). If they are equal, we change round to the value of the last bit (23rd) of the frac field.
The net effect of the code above is to modify the value of round to 0 when the rounded-off digits are in the form 10...0 and the last frac bit is also 0. This will round frac to an even value (least significant digit 0) when we’re equally distant from two rounding options.
Testing
This time we’ll test our converter in the range of values 100 million to 1 billion.
int main() {
int i;
float *fp;
float_bits f;
for (i=1e8; i<1e9; i++) {
f = float_i2f(i);
fp = &f;
if (*fp != (float) i)
printf("Casting not equal for value: %d\nConverted value is %.0f\nCasted value is %.0f\n", i, *fp, (float) i);
}
}
After compiling and executing we get some error messages:
Casting not equal for value: 134217724 Converted value is 67108864 Casted value is 134217728 ...
Our converter does not handle the value 134217724 (and many others) correctly. Checking its binary representation we get:
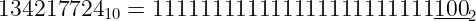
The digits that are rounded-off are underlined. We see that the frac field that corresponds to this value is all ones. We’ll need to handle this case differently.
Special case: frac field is all ones
When the frac field is all ones and it needs to be rounded, adding one to it will make it overflow. Let’s see an example:
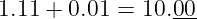
Here we have a number with a binary fraction consisting of all ones. If we add one to its least significant digit, the fraction part of it will change to all zeros. Moreover, the addition will overflow beyond the binary point.
In terms of the exp field, we’ll have the following:
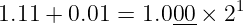
We can see that the exponent is incremented by one. Since float numbers are encoded in the form 1.XXX*2^y, when the frac field overflows, the exp field will be increased by one.
These changes can be readily applied into our converter:
/* Round to closest */
unsigned round = frac >> (E - 24) & 1;
/* Round-to-even modification */
unsigned last_frac_bit = frac >> (E - 23) & 1;
unsigned rounded_off_digits = frac << 2 + 30 - E + 23 >> 2 + 30 - E + 23;
unsigned one_followed_by_zeros = 1 << E - 24;
if (rounded_off_digits == one_followed_by_zeros)
round = last_frac_bit;
frac >>= E-23;
/* Special case: frac = 11...1 */
unsigned all_ones = -1 & 0x7FFFFF;
if (frac == all_ones && round) {
frac = 0;
exp++;
round = 0;
}
frac += round;
We included a conditional statement that makes the necessary changes when the frac field is all ones and needs to be rounded. In that case, we set frac to 0 and instead increment the exp field by one.
Testing
With this final changes, we’re ready to test the converter in the whole range of int values. Importing INT_MIN and INT_MAX from the limits.h library:
int main() {
int i;
float *fp;
float_bits f;
for (i=INT_MIN; i<INT_MAX; i++) {
f = float_i2f(i);
fp = &f;
if (*fp != (float) i)
printf("Casting not equal for value: %d\nConverted value is %.0f\nCasted value is %.0f\n", i, *fp, (float) i);
}
}
After compilation and execution, we get a single error message:
$ ./main Casting not equal for value: -2147483648 Converted value is -2 Casted value is -2147483648
This final error takes place because we cannot represent -INT_MIN using int (INT_MAX = abs(INT_MIN) - 1). We’ll handle this case differently.
Special case: INT_MIN
To handle this case, we’ll just set the E and M values for this single case:
/* Exponent */
unsigned E;
if (i != INT_MIN)
E = (int) (log(i<0 ? -i : i)/log(2));
else
/* INT_MIN = -1 * 2^31 */
E = 31;
unsigned exp = E + 127;
/* Magnificand*/
unsigned M;
if (i != INT_MIN)
M = i>0 ? i : -i;
else
/* INT_MIN = -1 * 2^31 */
M = 1<<31;
With this new changes, we’ll now present the whole program and test it for the whole range of int values.
Complete converter and final testing
The code for the converter, including all of the modification above, and testing for the whole range of int values is presented below.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <limits.h>
#define BIAS 127
#define K 23
typedef unsigned float_bits;
/* Convert 32-bits int to float */
float_bits float_i2f(int i) {
/* Special case : 0 is not a normalized value */
if (i==0)
return 0;
/* sign bit */
unsigned s = i>>31;
/* Exponent */
unsigned E;
if (i != INT_MIN)
E = (int) (log(i<0 ? -i : i)/log(2));
else
/* INT_MIN = -1.0 * 2^31 */
E = 31;
unsigned exp = E + BIAS;
/* Magnificand*/
unsigned M;
if (i != INT_MIN)
M = i>0 ? i : -i;
else
/* INT_MIN = -1.0 x 2^31*/
M = 1<<31;
unsigned frac = M ^ (1<<E);
/* Displace frac to start at bit position K=23 */
if (E>K) {
/* Frac field too long */
/* Round to closest */
unsigned round = frac >> (E - K - 1) & 1;
/* Round to even modification */
unsigned last_frac_bit = frac >> (E - K) & 1;
unsigned rounded_off_digits = frac << 32 - E + K >> 32 - E + K;
unsigned one_followed_by_zeros = 1 << E - K - 1;
if (rounded_off_digits == one_followed_by_zeros)
round = last_frac_bit;
/* Truncate to first 23th digits */
frac >>= E-K;
/* Special case: frac = 11..1 */
unsigned all_ones = -1 & 0x7FFFFF;
if (frac == all_ones && round) {
frac = 0;
exp++;
round = 0;
}
/* Round when necessary */
frac += round;
} else
/* Too short: Pad to the right with zeros */
frac <<= K-E;
return s<<31 | exp<<K | frac;
}
int main() {
int i;
float *fp;
float_bits f;
for (i=INT_MIN; i<INT_MAX; i++) {
f = float_i2f(i);
fp = &f;
if (*fp != (float) i)
printf("Casting not equal for value: %d\nConverted value is %.0f\nCasted value is %.0f\n", i, *fp, (float) i);
}
}
We have changed all instances of value 23 with K to denote that the frac field is K=23 bits long.
When we compile it and run it, we get no output message. This means that the presented converter correctly handles the whole range of int values just like C’s castin to float.